دلنوشت
۱
بررسی توابعی که با عبارات قدر مطلق بوجود میآیند
توابع گلدانی و سرسرهای
خلاصه :
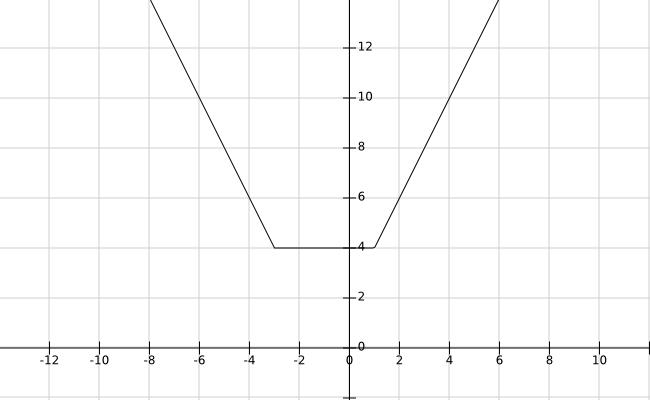
در جمع و تفریق بین دو عبارت قدر مطلق توابعی بوجود میآیند که ما این توابع را بررسی میکنیمتابع گلدانی: به تابعی میگویند که بین دو عبارت قدرت مطلق جمع شوند یعنی:|f(x)=|x-a|+|x-b
در این نوع نمودارها محور تقارن خط x=(a+b)/2
مانند:|f(x)=|x-۱|+|x+۳

همانطور که میبینید در نقاط a وb نمودار شکسته و در بین این دو نقطه ثابت است و قبل نقطه کوچکتر نزولی و بعد از نقطه بزرگتر صعودی است
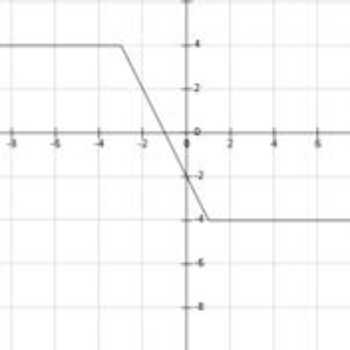
تابع سرسرهای:تابعی که بین دو عبارت قدر مطلق عملیات تفریق انجام میشود یعنی:|f(x)=|x-a|-|x-b
در این تابع نقطهی x=(a+b)/2 و y=0 نقطهی تقارن نمودار است
این نمودار قبل از کوچکترین نقطه و بعد از بزرگترین نقطه ثابت است و در بین این نقاط نزولی یا صعودی است
مانند:|f(x)=|x-۱|-|x+۳

که همونطور که میبینید در نقاط ۳- و ۱ نمودار شکسته ُبین دو محل شکست نزولی و قبل و بعد آن ثابت است










آقای مهدوی
۶ سال پیش