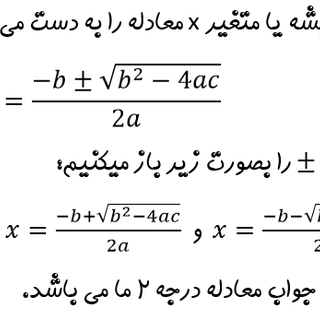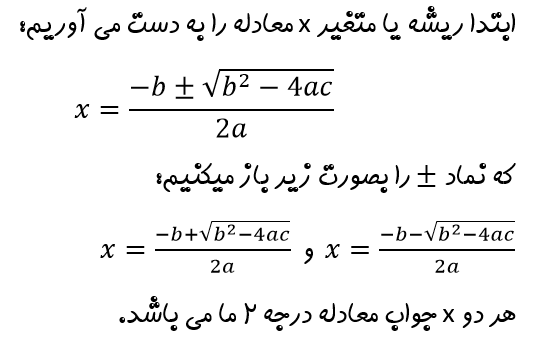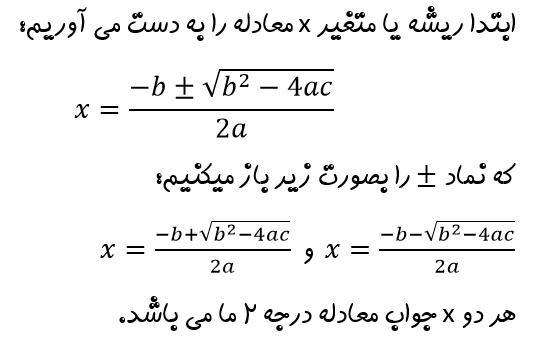
معرفی
۱
درس حساب (حل معادله درجه دوم و نکات کنکوری آن )
درس حساب (حل معادله درجه دوم و نکات کنکوری آن )
درس حساب (حل معادله درجه دوم و نکات کنکوری آن )
خلاصه :
نکات کنکوری معادله درجه دوم- روش های حل معدله درجه دوم به صرت کاملا مفید و خلاصه شده+ چند نکته کاربردی تستی ومهم
- امید خدام گرد آورنده: دبیر محتر م:جناب آقای جباری
- تعریف معادله درجه دو
- معادله ای است که بیشترین توان آن پس از ساده کردن 2 باشد، معادله درجه دوم
- نامیده میشود و فرم کلی آن به صورت زیر است:
- ax2+bx+c=0 , a≠0 , a,b,c∈R
- انواع روشهای حل معادله درجه دوم
- برای حل معادله درجه دم روشهای مختلفی است که مهمترین آنها عبارتند از:
- تجزیه
- روش ریشه گیری
- روش کلی یا Δ
- روش هندسی (رسم نمودار)
- روش تجزیه برای حل معادله درجه دوم
- تجزیه یک عبارت جبری یعنی عبارتی که به صورت جمع و تفریق هست را به شکل حاصلضرب عاملهای اول دربیاوریم. میدانیم هرعبارتی تجزیه پذیر به عاملهای اصلی نیست. پس روش تجزیه یک روش کلی برای حل معادله نخواهد بود. اما اگر معادله ای تجزیه پذیر باشد، میتوان آن را تجزیه کرد. و با استفاده از نکته های زیر ریشه های معادله (جوابها) را بدست آورد:
- ab=0 یا a=0 یا b=0
- فاکتور گیری یا استفاده از اتحادها، از رایجترین روشهای تجزیه برای حل معادله است.
- مثال از روش تجزیه برای حل معادله درجه دوم
- x2−3x=0
- در این معادله که c=0 می باشد، روش فاکتورگیری بهترین روش برای حل آن است و داریم:
- x(3−x)=0
- x=0 3−x=0 ⇒ x=3
- یا معادله x2+5x+6=0 را در نظر بگیرید. این معادله را میتوان با کمک اتحاد جمله مشترک که درنهایت منجر به حل معادله درجه دوم می شود تجزیه کرد:
- (x+2)(x+3)=0 ⇒ {xx==−2−3
- حتی گاهی معادلات با درجه های بالاتر را نیز به کمک تجزیه میتوان حل کرد مانند:
- x3−x=0
- x(x2−1)=0 ⇒ x(x−1)(x+1)=0
- x=0 x=1 x=−1
- در این مثال از فاکتوریگیری و اتحاد مزدوج برای تجزیه کمک گرفته شده است.
- روش ریشه گیری برای حل معادله درجه دوم
- معادله ی درجه دومی که b=0 باشد را در نظر بگیرید. مثل x2−9=0 . برای حل این معادله میتوان از دو روش تجزیه به کمک اتحاد مزدوج و ریشه گیری استفاده کرد. یعنی:
- x2=9 ⇒ x=±3
- در این روش مانند معادله درجه اول ابتدا مجهول را تنها میکنیم. سپس از دو طرف ریشه دوم میگیریم:
- 3x2−7=0 ⇒ x2=73 ⇒ x=±73−−√
- باید در این روش دقت کنیم وقتی مجهول را تنها کردیم نباید طرف دوم منفی باشد در این صورت معادله جواب ندارد. مانند:
- x2+4=0 ⇒ x2=−2 ریشه ندارد
- پس به طور کلی اگر x2=a به شرط آنکه x=±a−−√ ، x2+4=0 خواهد بود.
- مثال از ریشه گیری
- ریشه گیری درموارد زیر نیز کاربرد دارد مانند:
- (x−3)2=25
- این نیز یک معادله درجه دوم است که به راحتی با ریشه گیری قابل حل است:
- x−3=±5 ⇒ {x−3x−3==5−5⇒⇒xx=8=−2
- روش کلی برای حل معادله درجه دوم
- یا روش کلی یکی از مهمترین و رایج ترین راهها برای حل معادله درجه دوم میباشد که از رابطه زیر استفاده کنیم Δ
- Δ=b2−4ac
- بزرگتر از صفر باشد، پس نتیجه میگیریم معادله دو ریشه حقیق دارد که آنها را از رابطه زیر بدست می آوریم Δ اگر
- x=–b±Δ−−√2a
- باشد، معادله یک جواب دارد که از رابطه زیر بدست می آید Δ=0 اگر
- x= −b/2a
- کوچکتر از صفر باشد معادله ریشه حقیقی ندارد Δ>0 و اگر
- چند نکته کاربردی در مورد حل معادله درجه دوم
- اگر b=0 باشد، بهترین روش ریشه گیری میباشد:
- ax2+c=0 x=± √-c/a
- c/aبه شرطی که : 0<
- در روش تجزیه و روش کلی حتماً باید تمام متغیرها یکطرف برده شود و طرف دیگر صفر باشد.
- اگر در یک معادله درجه دوم جمع ضرایب صفر باشد یعنی:
- a+b+c=0
- c/a آنگاه یکی از ریشه ها 1 و دیگری
- x=1 , x=c/a
- اگر در یک معادله درجه دوم جمع ضرایب به صورت زیر باشد:
- a+c=+b
- -c/a آنگاه یه ریشه1 – و دیگری
- اگر در معادله درجه دوم b زوج باشد، علاوه بر روش Δ از روش Δ′ نیز میتوان استفاده کرد. پس داریم :
- b′= b/2 , Δ′= (به توان دو)b′2−ac , x= –b′± √ Δ′/a
- هرگاه در معادله درجه دومی a و c مختلف العلامت باشند، معادله حتماً دو ریشه متمایز حقیقی دارد ( Δ بزرگتر از صفر).