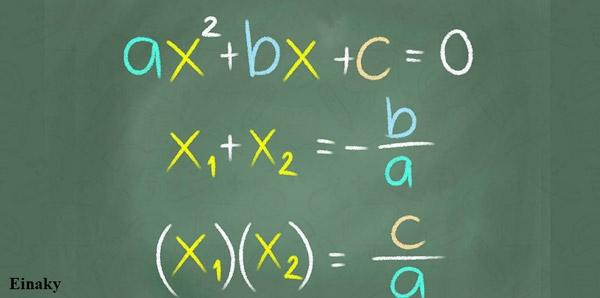
محتوای درسی
معادله درجه۲
اموزش
خلاصه :
نگاهی به معادله درجه ۲بسم الله الرحمن الرحیم
شکل معادله درجه دوم
جهت تعیین درجه یک معادله به بزرگترین توانِ متغیرِ آن نگاه کنید. اگر بزرگترین توان ۲ باشد، معادله نیز از مرتبه دوم یا به عبارتی از درجه دو است. برای نمونه معادله زیر یک معادله درجه دوم است چراکه بزرگترین متغیرِ (در این معادله x متغیر است) موجود در آن برابر با ۲ است.
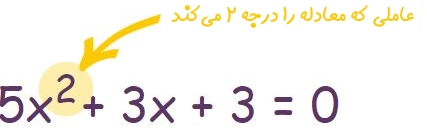
منحنی معادلات درجه دوم بهشکل زیر هستند.
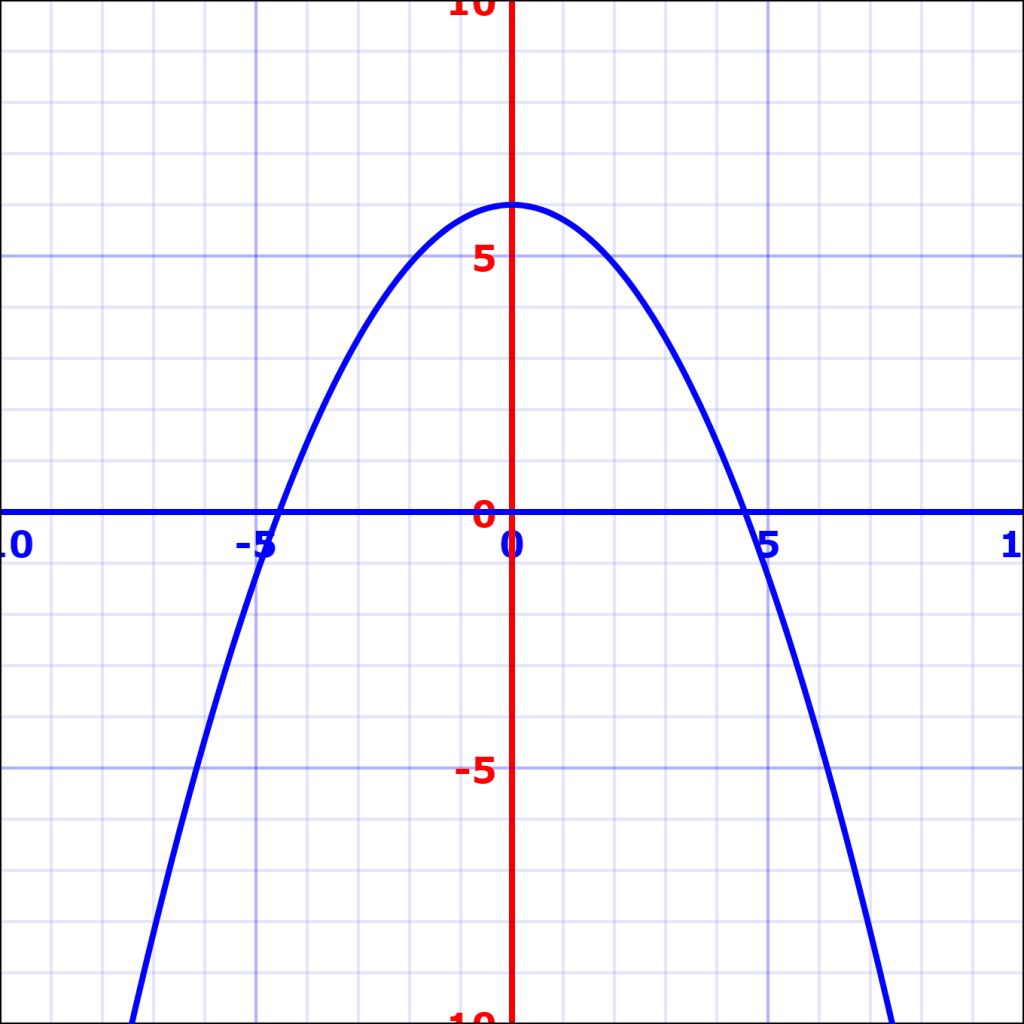
البته توجه داشته باشید که خمیدگی منحنی ممکن است به سمت بالا نیز باشد.
شکل استاندارد
معمولا شکل استاندارد معادلات درجه دو بهصورت زیر بیان میشوند:
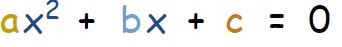
در رابطه بالا ضرایب a,b,c ثابت بوده و مقدار a غیرصفر است. همچنین x همان مجهولی است که هدف از حل کردن معادله یافتن آن است. در جدول زیر مثالهایی از معادلات درجه دوم ارائه شده است.

توجه داشته باشید که در مواقعی ممکن است شکل اولیهی معادله بهصورت استاندارد نباشد. در چنین حالاتی میتوان با جابجایی عبارات در طرفین معادله، شکل معادله را بهصورت استاندارد درآورد.
برای نمونه در جدول زیر تعدادی معادله ارائه شده که شکل اولیه آنها استاندارد نیست. همانطور که میبینید، در ستون سوم، شکل استاندارد این معادلات ارائه شده است.
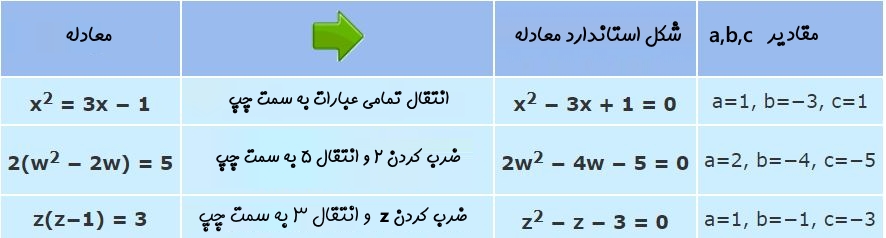
حل معادله درجه دوم
منظور از پاسخ معادلهی درجه دوم، مقداری از x است که به ازای آن، پاسخ معادله برابر با صفر شود. برای نمونه معادله x2-1=0 را در نظر بگیرید. اگر x=1 را در این معادله قرار دهیم، مقدار آن برابر با ۰=۱-۱۲ خواهد شد. بنابراین x=1 پاسخی برای معادله فوق محسوب میشود. توجه داشته باشید که یک معادله درجه دوم معمولا دارای دو پاسخ است. برای نمونه x=-1 نیز پاسخ معادله x2-1=0 است. حال معادلهای به شکل استاندارد (ax2+bx+c=0) را تصور کنید. در حالت کلی سه روش بهمنظور حل این معادله وجود دارد:
- فاکتورگیری
- مربع کامل
- استفاده از فرمول زیر
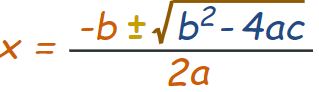
رابطه ۱
برای آشنایی بیشتر با فاکتورگیری و تجزیه چند جملهایها به مبحث «اتحاد و تجزیه در ریاضی — به زبان ساده» مراجعه کنید.
اثبات پاسخ بدست آمده
شاید به نحوه یافتن رابطهی ارائه شده در روش شماره ۳ علاقهمند باشید. در ابتدا پیشنهاد میشود مطلبِ معادله دایره را مطالعه فرموده و در مورد نحوه بدست آمدن پاسخ شماره ۳ فکر کنید.
در اولین قدم طرفین رابطه را به a تقسیم کنید. با انجام این کار رابطه استاندارد بهصورت زیر در میآید.
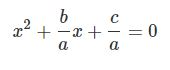
در قدم بعدی به طرفین رابطهی بالا، عدد b24a2b24a2 را اضافه کنید. در نتیجه شکل عمومی رابطه فوق برابر خواهد بود با:
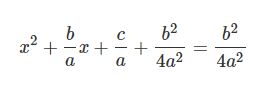
b24a2b24a2 را نگه داشته و c/a را به سمت راست منتقل میکنیم. با انجام این کار رابطه بالا بهشکل زیر در میآید.
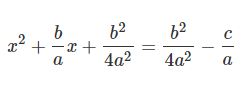
با توجه به مطلب معادله دایره، رابطه بالا یک دایره به شعاع √b24a2−cab24a2−ca را نشان میدهد. در حقیقت میتوان رابطه بالا را به شکل زیر بازنویسی کرد.
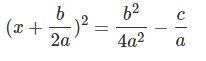
جهت بدست آوردن پاسخ x، از طرفین رابطه بالا جذر گرفته و آن را بهصورت زیر بازنویسی میکنیم.
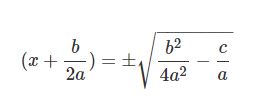
با نگه داشتن x و بردن b/2a به سمت راست، پاسخ x برابر با رابطه زیر بدست میآید.
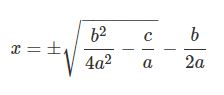
با فاکتور گرفتنِ ۱/۲a از سمت راستِ رابطهی بالا داریم:
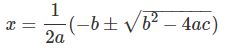
معمولا عبارت b2−4acb2−4ac را بهصورت جداگانه با علامت ΔΔ (دلتا) نمایش میدهند؛ با این فرض رابطه فوق بهصورت زیر در خواهد آمد.
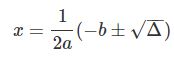
توجه داشته باشید که علامت ± به معنای این است که معادله درجه دوم دارای دو پاسخ است. در حقیقت محل تلاقی نمودار درجه دوم با محور xها همان پاسخ معادله است. همانطور که در شکل زیر نیز میبینید نمودار درجه دوم در دو نقطه محور xها را قطع کرده است.
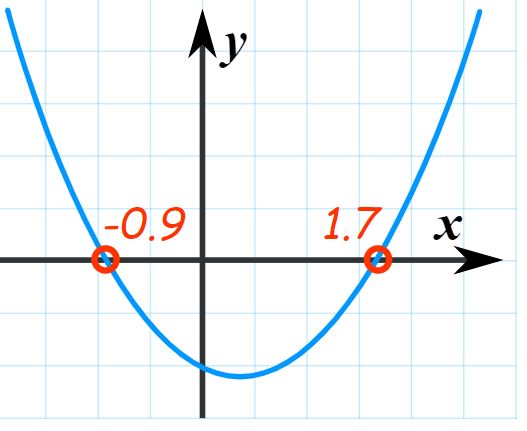
اما اگر کل نمودار بالای محور xها قرار گیرد، نمودار محورها xها را در نقطهای قطع نمیکند؛ بنابراین پاسخها به چه شکل خواهند بود؟ در ادامه در این مورد توضیح خواهیم داد.
حالتهای مختلفِ ΔΔ
همانطور که در بالا نیز اشاره شد، در پاسخ x عبارت b2-4ac یا همان دلتا زیر رادیکال قرار میگیرد، در نتیجه این مقدار هر عددی نمیتواند باشد چراکه مقدار زیر رادیکال بایستی بیشتر از صفر باشد (۰< ΔΔ). نهایتا برای یک معادله درجهی دوم حالتهای زیر میتواند رخ دهد:
- b2-4ac مثبت باشد. در این حالت معادله دو پاسخ متفاوت دارد.
- b2-4ac صفر باشد. در این حالت معادله دو پاسخ مشابه یا اصطلاحا ریشه مضاعف دارد.
- b2-4ac منفی باشد. در این حالت معادله پاسخی ندارد.
مثال ۱
پاسخ معادله 5x2+6x+1=0 را بیابید.
جهت حل یک معادلهی درجه دوم در ابتدا بایستی ضرایب a,b,c را بیابید. با مقایسه معادله مذکور با معادله ax2+bx+c=0 مقادیر a,b,c برابر با اعداد زیر بدست میآیند.
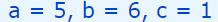
در قدم بعدی بایستی Δ را محاسبه کرده و علامت آن را مشخص کنید. با توجه به مقادیر a,b,c اندازه Δ برابر است با:
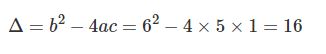
عدد بالا مثبت است؛ در نتیجه این معادله دارای دو پاسخ متفاوت خواهد بود. با استفاده از رابطه ۱، پاسخ معادله برابر است با:
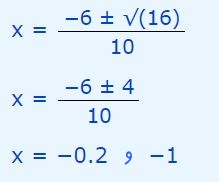
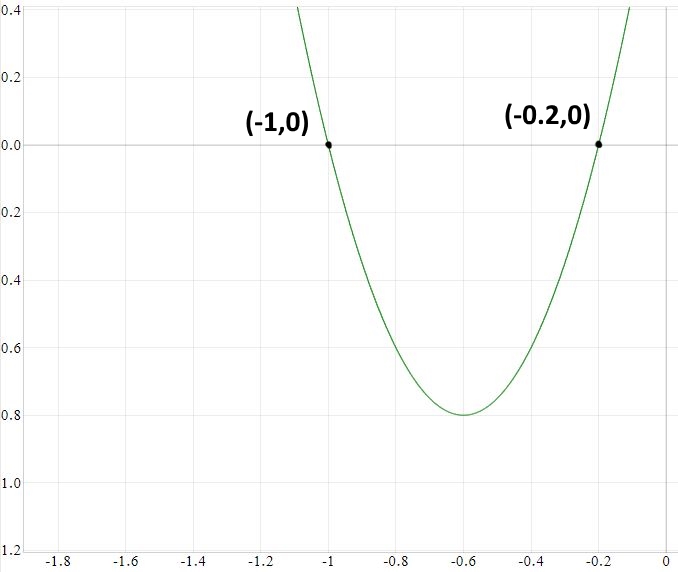
همانطور که انتظار میرفت معادله فوق دارای دو پاسخ است. البته نمودار رابطه فوق نیز همین امر را نشان میدهد. در حقیقت نمودار رابطه فوق بهشکل زیر است.
مثال ۲
پاسخ معادله 5x2+2x+1=0 را بیابید.
در رابطه فوق مقادیر a,b,c برابرند با:
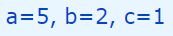
در نتیجه دلتا برابر است با:
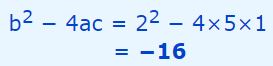
مقدار دلتای بدست آمده منفی است؛ بنابراین معادله فوق پاسخی در اعداد حقیقی ندارد.
خلاصه
- شکل عمومی یک معادله درجه دو بصورت ax2+bx+c=0 است.
- پاسخهای یک معادله درجه ۲ برابرند با:
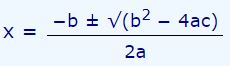
- در صورت مثبت بودن دلتا (0<b2−4ac0<b2−4ac)، معادله دارای دو پاسخِ متفاوت است.
- در صورتی که دلتا منفی باشد، معادله پاسخی ندارد.
- در صورتی که دلتا برابر با صفر باشد، معادله دو پاسخ یکسان یا اصطلاحا ریشه مضاعف دارد.





AMIR.ena
۶ سال پیش