خلاصه :

تابع گلدانی

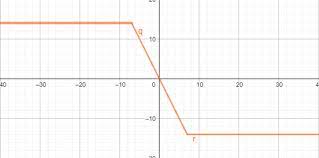
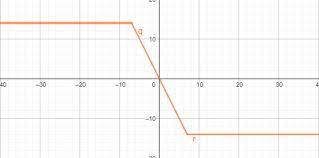
تابع گلدانی به خاطر اینکه به صورت سه بخشی رسم میشه و محل برخورد این سه بخش چیزی شبیه به گلدان است به توابع گلدانی شناخته میشن.

معادله ی این نوع از توابع از جمع دو قدر مطلق دارای ایکس که منهای یک متغیر دیگه میشن به دست میاد

f(x)=|x-a|+|x-b|

این معادله در واقع به سه بخش تقسیم میشه:

(فرض میکنیم که b بیشتر از a باشه)

حالا اگه x<b باشه(که نتیجه اش x<a هم هست)معادله مون این شکلی میشه:

f(x)=2x-(a+b)

(در واقع هیچ کدوم از قدر مطلق ها اثر نکردند)

اگر که  b ⩾ x ⩾ a بود اون وقت یکی از قدر مطلق ها عمل میکنه و معادله مون این شکلی میشه:

f(x)=x-a -x +b= b-a

اگرم x<a بود هر دو قدر مطلق عمل میکنن و خواهیم داشت:

f(x)=-2x+(a+b)

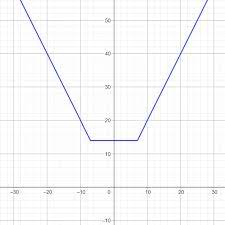
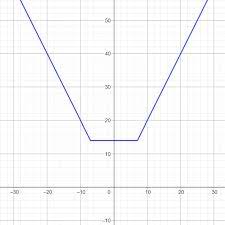
حالا رسم سریعش رو باهم میبینیم:

1. b-a رو حساب می کنیم

2. نقاط x=b  و x=a رو علامت میزنیم

3. شیب دو پاره خط متصل رو حساب میکنیم(دو برابر ضرایب x و قرینه هم)

4. حالا پاره خطی در y=b-a از x=a تا x=b میکشیم و دو پاره خط رو با شیبی که به دست آوردیم به اون وصل میکنیم

تابع سرسره ای

این تابع هم بسیار شبیه به تابع گلدانیه فقط به جای اینکه قدر مطلق ها با هم جمع بشن از هم کم میشن

f(x)=|x-a|-|x-b|

این معادله هم در واقع به سه بخش تقسیم میشه:

حالا اگه x<b باشه(که نتیجه اش x<a هم هست)معادله مون این شکلی میشه:

f(x)=x-a-x+b=b-a

(در واقع هیچ کدوم از قدر مطلق ها اثر نکردند)

اگر که  b ⩾ x ⩾ a بود اون وقت یکی از قدر مطلق ها عمل میکنه و معادله مون این شکلی میشه:

f(x)=x-a +x -b= 2x-(b-a)

اگرم x<a بود هر دو قدر مطلق عمل میکنن و خواهیم داشت:

f(x)=-x+a+x-b=a-b

رسمش حتی از تابع گلدانی هم ساده تره:

کافیه a و   b رو تو معادله مون بزاریم دو تا نقطه ای که بدست اومد رو بهم وصل میکنم و نقاطی که بدست آورده بودیم رو موازی خط x ها تا مثبت و منفی بی نهایت ادامه میدیم