توابع گلدانی و سرسره ای

خلاصه :

در این مطلب با دو تابع گلدانی و سرسره ای بیشتر آشنا می شویم.

تابع گلدانی

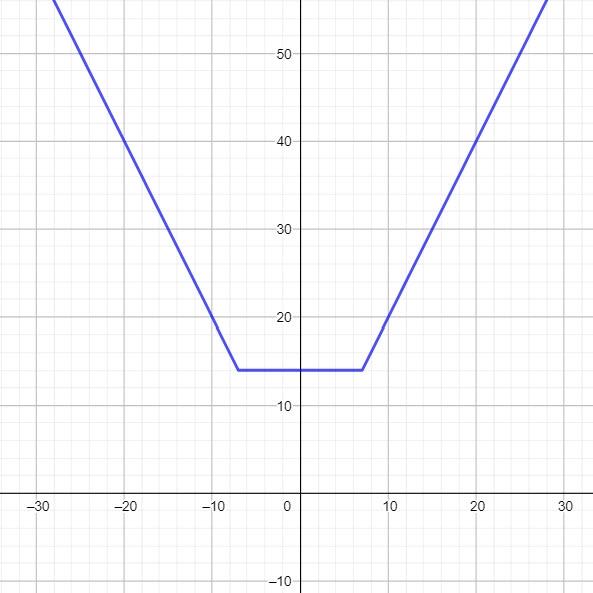
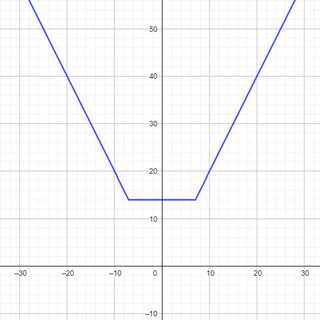
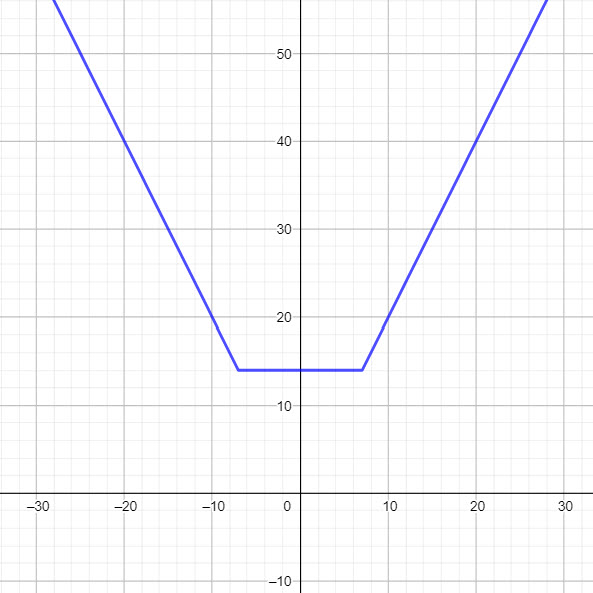
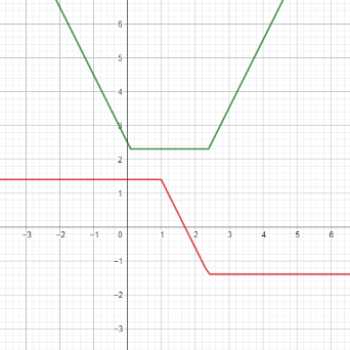
ضابطه ی این تابع به صورت |f(x)=|x-a|+|x-b می باشد که در آن ضرایب x مشابه است. علت نامگذاری این تابع به تابع گلدانی به دلیل شباهت شکل نمودار آن به گلدان است. اگر این تابع را به صورت چند ضابطه ای بنویسیم، خواهیم دید که محل اتصال سه نمودار یا به عبارتی دیگر محل شکستگی های نمودارمان برابر با نقاط x=a و x=b خواهد بود. از این موضوع می توان به یافته های فراوان رسید.

با شرط a < b نمودار در بازه a<x<b به صورت خطی با فرمول y=b-a می باشد و به طور کلی اندازه ی آن نیز با فرمول |a-b| قابل محاسبه است.

البته نیاز چندانی به دانستن فرمول این خط نیست و با جاگذاری طول a و b، عرض آنان نیز یافت می شود. با یافتن عرض این خطوط می توان برد تابع را نیز مشخص کرد ، بنابراین برد تابع |a-b| می شود. دامنه ی آن نیز که برابر با مجموعه اعداد حقیقی می باشد.

طبیعی است که وسط این پاره خط، محور تقارن این تابع خواهد بود، یعنی a+b)/2)

شیب دو نیم خط متصل به پاره خط زیرین نمودار برابر با دو برابر ضرایب x و قرینه ی یکدیگر است.

با این توصیفات رسم سریع این نمودار با جاگذاری مقادیر a و b به جای x آغاز شده و با وصل آنان پاره خط پایه ی گلدانمان را به دست می آوریم. سپس با شیب گفته شده دیواره های گلدانمان را به سوی مثبت و منفی بی نهایت رسم می کنیم.

تابع سرسره ای

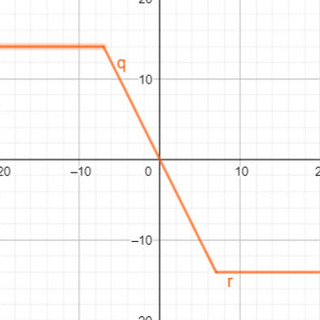
علت نام گذاری این تابع نیز به دلیل شکل نمودار آن است و ضابطه ی آن به صورت زیر می باشد:

|f(x)=|x-a|-|x-b

اگر این تابع را به صورت چند ضابطه ای بنویسیم خواهیم دید که طول نقاط اتصال سه نمودار یا به عبارتی دیگر طول محل شکستگی نمودار برابر با a و bخواهد بود .

به صورت جبری هم می توان به این رسید که در بین نقاط گفته شده، نزولی یا صعودی است و در باقی به صورت خط ثابت می باشد.

پس باز هم خط تقارن تابع سرسره ای برابر با آنچه در مورد خط تقارن تابع گلدانی گفته شده است، می باشد و همانطور که دامنه ی آن مجموعه اعداد حقیقی است، برد آن بین عرض دو نقطه خواهد بود. عرضشان هم که با جاگذاری طول هایشان به جای x به دست می آید.

پس رسم این تابع حتی از رسم تابع گلدانی نیز راحت تر خواهد بود. a و b را در فرمول جاگذاری می کنیم تا مختصات نقاط شکستگی به دست آید. نقاط را به هم وصل می کنیم و از دو سر پاره خط نیم خط هایی را به صورت عرض ثابت تا مثبت و منفی بی نهایت به گونه ای رسم می کنیم که شکل تابع باشد.