آموزش
عدد اول چیست و چرا اهمیت دارد؟
خلاصه :
اعداد اول را از دوران تحصیل میشناسیم. با اینحال کاربرد این اعداد بسیار فراتر از ریاضیات است و نقش بهسزایی در زندگی ما ایفا میکند.اگر خاطرات مبهمی از ریاضیات مدرسه دارید، ممکن است اعداد اول را به یاد نیاورید. اعداد اول علاوهبر ریاضیات، اهمیت زیادی در کاربردهای زندگی روزمره دارند بهطوریکه برای امن نگهداشتن ایمیلها در مقابل هکرها یا جستجوی ایمن وب روی شبکهی خصوصی مجازی (VPN)، بدون اینکه بدانید از اعداد اول استفاده میکنید. اعداد اول بخش مهمی از رمزنگاری RSA به شمار میروند و بهعنوان کلیدهایی برای رمزگشایی پیغامهای مخفی در متنهای نامفهوم دیجیتالی به کار میروند.
تعریف عدد اول
عدد اول به عدد مثبت بزرگتر از یک گفته میشود که تنها بر خودش و یک بخشپذیر ست. با توجه به این تعریف، عدد ۱، عدد اول نیست.
روشی مناسب برای به خاطر سپردن اعداد اول این است که این اعداد بر هیچ عدد مثبت طبیعی دیگری بخشپذیر نیستند و در صورت تقسیم دارای باقیمانده خواهند بود. برای مثال عدد ۱۳ را در نظر بگیرید که بر یک و خودش بخشپذیر است و اگر برای مثال بر ۶ تقسیم شود، باقیماندهی ۱ به دست خواهد آمد.
اعداد اول تنها بر خودشان و عدد یک بخشپذیر هستند
تفاوت اعداد اول و اعداد مرکب
اعداد مرکب دقیقا در نقطهی مقابل اعداد اول قرار دارند. این اعداد علاوهبر یک و خودشان بر اعداد دیگر هم بخشپذیرند. برای مثال عدد ۶ عددی مرکب است چرا که علاوه بر یک و خودش بر اعداد ۲ و ۳ نیز بخشپذیر است.
ویژگیهای عدد اول
اگر مطمئن نیستید عددی اول است باید ویژگیهای زیر را در آن پیدا کنید.
- تنها بر خود و ۱ بخشپذیر است. این تعریف قدیمی اعداد اول و اولین چیزی است که باید در محاسبهی اعداد اول به دنبال آن باشید.
- عدد مثبت است. اعداد اول همیشه مثبت هستند زیرا اعداد مثبت تنها اعدادی هستند که میتوانند دو ضریب داشته باشند. برای مثال عدد ۳ دارای دو ضریب ۱ و ۳ است. از طرفی عدد منفی ۳ دارای چهار ضریب است که عبارتاند از ۱، ۳، ۱- و ۳.
- عدد بزرگتر از ۱ است. تنها ضریب عدد ۱ خودش است. در نتیجه یک تنها دارای یک ضریب است و اعداد اول باید دو ضریب داشته باشند.
- عدد باید فرد باشد. به جز عدد ۲ که تنها عدد اول زوج است، تمام اعداد اول فرد هستند؛ زیرا اعداد زوج معمولاً بیش از دو ضریب دارند.
روشهای پیدا کردن عدد اول
بهطورکلی روشهای متعددی برای تشخیص اول بودن یک عدد وجود دارند. بهترین روش برای یافتن اعداد اول، روش تجزیه یا فاکتورگیری است. با روش فاکتورگیری، ضریبهای یک عدد به دست میآیند و به این ترتیب بهراحتی میتوان یک عدد اول را شناسایی کرد.
پیدا کردن عدد اول به روش فاکتورگیری
فاکتورگیری بهترین روش برای پیدا کردن اعداد اول است. مراحل این روش عبارتاند از:
- مرحله ۱: اولین ضریبهای یک عدد مشخص را پیدا کنید.
- مرحله ۲: تعداد ضریبهای آن عدد را بررسی کنید.
- مرحله ۳: اگر تعداد ضریبها بیش از دو باشد، عدد اول نیست.
مثال: عدد ۳۶ را در نظر بگیرید. ۳۶ را میتوان بهصورت ۲*۳*۲*۳ نوشت؛ بنابراین ضریبهای ۳۶ در اینجا عبارتاند از ۱، ۲، ۳، ۴، ۶، ۹، ۱۲، ۱۸ و ۳۶. ازآنجاکه تعداد ضریبهای ۳۶ بیشتر از ۲ است، این عدد اول نیست و عددی مرکب است.
حالا عدد ۱۹ را در نظر بگیرید. فاکتورگیری اول ۱۹ برابر است با ۱*۱۹. اینجا مشاهده میکنید که تنها دو ضریب برای ۱۹ وجود دارد، بنابراین عدد اول است.
چگونه میتوان تشخیص داد عددی بزرگ اول است؟
فرمولهایی برای یافتن اعداد اول وجود دارند. برای بررسی اول بودن یک عدد بزرگ، مراحل ذیل را دنبال کنید.
- مرحله ۱: جایگاه یکان عدد را بررسی کنید. اگر عدد به ۰، ۲، ۴، ۶ و ۸ ختم شد. اول نیست.
- مرحله ۲: رقمهای عدد را با یکدیگر جمع بزنید. اگر مجموع رقمها بر سه بخشپذیر بود، عدد اول نیست.
- مرحله ۳. پس از تأیید غلط بودن مراحل ۱ و ۲، ریشهی مربع عدد را پیدا کنید.
- مرحله ۴: عدد را بر تمام اعداد اول زیر مقدار ریشهی مربع تقسیم کنید.
- مرحله ۵. اگر عدد بر هرکدام از اعداد اول کمتر از ریشهی مربع خود بخشپذیر بود، اول نیست، اما در غیر این صورت اول است.
استثناء: اگر عددی بزرگی به ۵ ختم شد، همیشه بر ۵ بخشپذیر است. ازاینرو نمیتواند اول باشد.
غربال اراتوستن
غربال اراتوستن روشی است که توسط ریاضیدان یونانی، اراتوستن در قرن سوم پیش از میلاد برای جستجوی اعداد اول و مرکب از میان گروه مشخصی از اعداد معرفی شد. غربال اراتوستن مبتنیبر این ایده است که حاصل ضرب اعداد اول، اول نیست؛ بنابراین هنگام جستجوی اعداد اول، تمام ضربهای هر عدد اول را میتوان حذف کرد. به این ترتیب تعداد زیادی از اعداد حذف میشوند و در زمان صرفهجویی خواهد شد.
غربال اراتوستن، روشی کهن برای محاسبه اعداد اول است
اهمیت عدد اول
اعداد اول در بسیاری از حوزههای ریاضیات بهویژه نظریهی اعداد، رمزنگاری و علوم کامپیوتر حائز اهمیت هستند. در ادامه به دلایل اهمیت این اعداد اشاره میکنیم:
اجزای سازنده اعداد
اعداد اول را میتوان اجزای سازنده تمام اعداد مثبت در نظر گرفت. هر عدد مثبت صحیح را میتوان به شکل محصولی از اعداد اول به شیوهای منحصربهفرد در نظر گرفت که به نظریهی بنیادین حساب معروف است. برای مثال عدد ۱۲ را میتوان به شکل فرآوردهای از اعداد اول ۲، ۲ و ۳ در نظر گرفت بهطوریکه 2*2*3=12.
رمزنگاری
اعداد اول به شکل گستردهای در رمزنگاری مدرن به کار میروند. رمزنگاری در ایمنسازی ارتباطات کاربرد دارد. اعداد اول را میتوان در الگوریتمهای RSA به کار برد که برای ایمنسازی انتقال دادهها روی اینترنت به کار میروند.
اعداد اول کاربرد گستردهای در الگوریتم رمزنگاری RSA دارند
فاکتورگیری
فاکتورگیری اول به فرآیند نمایش یک عدد صحیح به شکل حاصل ضریبهای اول گفته میشود. برای مثال، فاکتورگیری اول ۱۲ برابر است با ۲*۲*۳. فاکتورگیری اول برای حل بسیاری از مسئلهها در نظریهی اعداد و رمزنگاری حائز اهمیت است.
اعداد اول در طبیعت
اعداد اول در طبیعت هم ظاهر میشوند. برای مثال، گونههای جیرجیرکهای دشتی در آمریکای شمالی هر ۱۳ الی ۱۷ سال ظاهر میشوند که نمونهای از چرخههای مبتنی بر عدد اول است و به فرار آنها از دست شکارچیان کمک میکند.
کاربردهای عدد اول
یکی از مهمترین کاربردهای اعداد اول، امنیت سایبری است که باعث میشود اطلاعات با امنیت بیشتری در اینترنت به اشتراک گذاشته شوند. برای ایمنسازی چیزهایی مثل جزئیات کارتها و رمزها، سوابق پزشکی و حتی سرویسهای پیامرسانی مثل واتساپ، مهندسین نرمافزار با استفاده از اعداد اول، الگوریتمهای خود را میسازند.
با ضرب دو عدد اول بزرگ میتوان به اعداد بزرگتری رسید که ضریبهای اصلی آنها برایمان شناخته شده باشند. برخی شرکتها از اعداد اول با صدها رقم برای رمزنگاری اطلاعات خود استفاده میکنند. اگر شخصی بخواهد به اطلاعات ارسالی شما دسترسی داشته باشد، باید ضریبهای اصلی را پیدا کند. با وجود اعداد اول طولانی، پیدا کردن این ضریبها سالها یا حتی دهها سال به طول میانجامد. از دیگر کاربردهای اعداد اول میتوان به موارد ذیل اشاره کرد:
- اعداد اول در تولید کدهای تصحیح خطا در ارتباط راه دور نیز کاربرد دارند. این اعداد تضمین میکنند که پیام با تصحیح خودکار ارسال و دریافت شده است.
- اعداد اول در بلاکچین برای ایجاد مقادیر منحصربهفرد توابع هش به کار میروند.
- اعداد اولی برای تولید اعداد شبه تصادفی به کار میروند.
- اعداد اول همچنین در طراحی ماشینهای روتوری کاربرد دارند. این اعداد به تولید یک چرخهی کامل پیش از تکرار موقعیتهای احتمالی روتور کمک میکنند.
مثالهای عدد اول
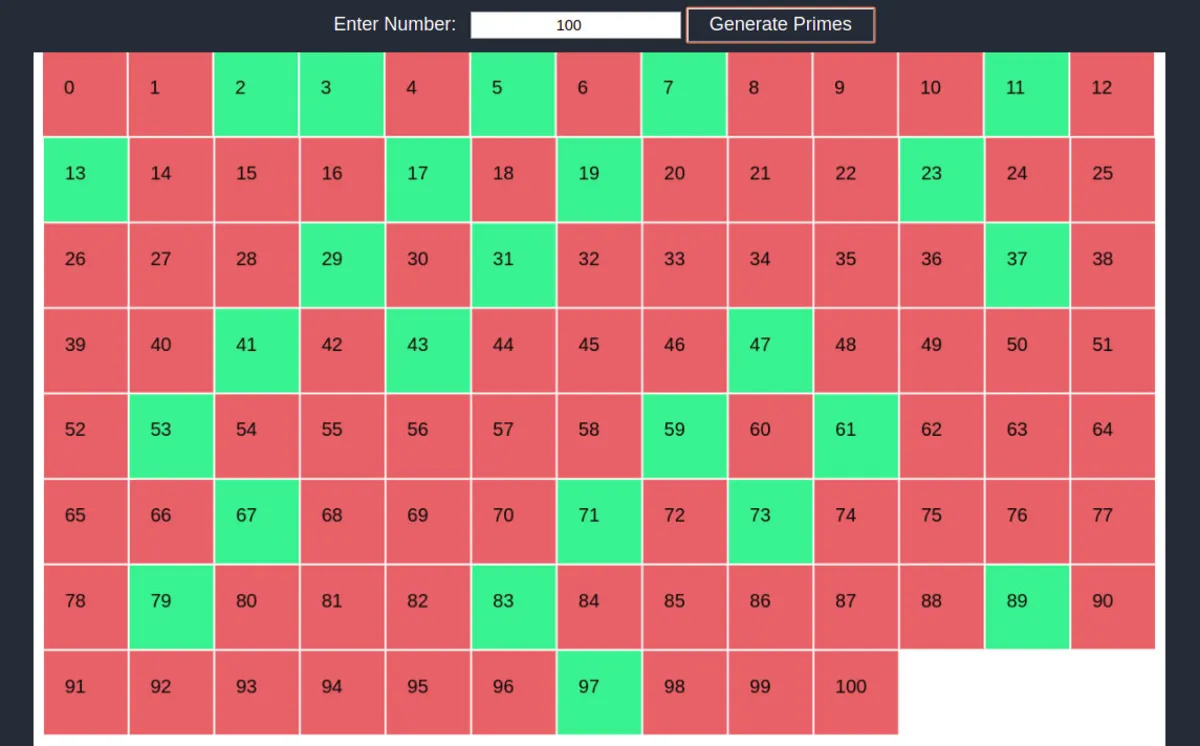
۲۵ عدد اول تا ۱۰۰ وجود دارند. فهرست اعداد اول تا ۱۰۰ عبارتاند از: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹، ۲۳، ۲۹، ۳۱، ۳۷، ۴۱، ۴۳، ۴۷، ۵۳، ۵۹، ۶۱، ۶۷، ۷۱، ۷۳، ۷۹، ۸۳، ۸۹، ۹۷.
اعداد مرسن، نمونهی دیگری از اعداد اول هستند که فرمول آنها به این صورت است: Mn = 2n – 1. در اینجا n یک عدد صحیح است. برای مثال عدد ۳ یک نوع عدد مرسن است زیرا برابر است با: 2^2-1. هفت عدد اول مرسن بعدی عبارتاند از: ۷ (n=3)، ۳۱ (n=5)، ۱۲۷ (n=7)، ۸۱۹۱ (n=13)، ۱۳۱٬۰۷۱ (n=17)، ۵۲۴٬۲۸۷ (n=19) و ۲٬۱۴۷٬۴۸۳٬۳۶۷ (n=31).
نام اعداد مرسن برگرفته از نام مارین مرسن، کشیش و ریاضیدان فرانسوی است که در قرن هفدهم به بررسی این اعداد پرداخت. فرمول اعداد مرسن همچنین برای کشف بزرگترین اعداد اول به کار میرود.
فهرست اعداد اول تا ۱۰۰
حقایق جالب درباره اعداد اول
حقایقی دربارهی اعداد اول وجود دارند که معمولاً سر کلاس درس به شما نمیگویند. در ادامه به برخی از جذابترین حقایق دربارهی اعداد اول میپردازیم.
به باور برخی افراد، فرازمینیها سعی میکنند از طریق اعداد اول با ما ارتباط برقرار کنند
یکی از عجیبترین حقایق دربارهی اعداد اول را کارل ساگان نقل میکند. او در کتاب ۱۹۸۵ خود با عنوان «تماس» مدعی شد که فرازمینیها سعی میکنند با استفاده از اعداد اول به عنوان سیگنال، با انسانها ارتباط برقرار کنند.
اعداد اول برای اولین بار توسط ریاضیدانهای یونانی بررسی شدند
گرچه اولین شواهد مکتوب از اعداد اول در یک پاپیروس ریند در مصر ۱۵۵۰ پیش از میلاد کشف شدند، یونانیان باستان اولین افرادی بودند که بهصورت کامل به بررسی ویژگیهای اعداد اول پرداختند. اقلیدس از اسکندریه پیشتاز بررسی اعداد اول بود و بعدها بهعنوان پدر هندسه شناخته شد. اغلب دانش بنیادی که دربارهی اعداد اول داریم توسط اقلیدس تنظیم شده است.
بزرگترین عدد اول دارای بیش از ۲۴ میلیون رقم است
بزرگترین عدد اول شناخته شده، عدد 1- 82,589,933 ^2 است که در تاریخ ۷ دسامبر ۲۰۱۸ کشف شد و بیش از ۲۴ میلیون رقم دارد. این عدد که M82889933 نامیده میشود از گروه اعداد مرسن است.
۲ تنها عدد اول زوج است
۲ عدد اول درنظر گرفته میشود زیرا تنها بر خودش و ۱ بخشپذیر است. تمام اعداد زوج بر ۲ بخشپذیرند و به همین دلیل ۲ تنها عدد زوج اول و همچنین کوچکترین عدد اول است.
عدد ۲ تنها عدد زوج اول است
اعداد غیرمرکب، نام دیگر اعداد اول است
اعداد مرکب اعدادی با ضریبهای متعدد هستند. بر اساس این اصل تمام اعداد غیر از ۲، عدد مرکب به شمار میروند.
سازمانی برای جستجوی بزرگترین اعداد اول وجود دارد
جستجوی عظیم اینترنتی عدد اول مرسن (GIMPS) در سال ۱۹۹۶ توسط جورج ولتمن تأسیس شد. این سازمان از زمان تأسیس تا کنون ۵۱ عدد اول جدید و همچنین بزرگترین اعداد اول را شناسایی کرده است.
غربال اراتوستن قدیمیترین روش یافتن اعداد اول است
در سال ۲۰۰ پیش از میلاد، اراتوسنس ریاضیدان یونانی الگوریتمی را برای محاسبهی اعداد اول ایجاد کرد که غربال اراتوستن نامیده شد.
اعداد اول از زمان باستان با باورهای خرافی در ارتباط بودند
اعداد اول به دلیل ماهیت منحصربهفردشان از دیرباز مورد توجه بودند. ۷ یکی از اعداد اول مرتبط با خرافات است که برخی افراد آن را عددی کامل میدانند. در مقابل، ۱۳ به عنوان عددی منفی و شوم در نظر گرفته میشود.
با بزرگ شدن اعداد، اعداد اول کمیاب میشوند
اعداد اول دو رقم بهراحتی کشف میشوند اما هرچقدر اعداد بزرگتر شوند، فرآیند جستجوی اعداد اول هم دشوارتر خواهد شد. در اعداد بسیار بزرگ بهندرت به اعداد اول برمیخوریم.
محبوبترین عدد دنیا یک عدد اول است
بسیاری از افراد از عدد هفت با عنوان عدد شانس یاد میکنند. عدد ۷ وجههی مثبتی در کتاب مقدس دارد. منحصربهفرد بودن ۷ باعث شده به محبوبترین عدد جهان تبدیل شود.
اعداد اول که تفاضلشان برابر با دو باشد، اعداد اول دو قلو نامیده میشوند
اعداد اولی که حاصل تفریقشان برابر با ۲ باشد، اعداد اول دوقلو نامیده میشوند. از این مجموعه میتوان به این اعداد اشاره کرد: (۳،۵)، (۵،۷)، (۱۱،۱۳)، (۱۷،۱۹)، (۲۹،۳۱)، (۴۱،۴۳)، (۵۹، ۶۱)، (۷۱،۷۳)، (۱۰۱،۱۰۳)، (۱۰۷،۱۰۹)، (۱۳۷،۱۳۹).
اعداد اول نامتناهی هستند
اعداد اول به رقم خاصی محدود نمیشوند و نامتناهی هستند. بااینحال با افزایش تعداد رقمها، یافتن آنها دشوارتر میشود.
هیچ عدد اول بزرگتر از ۵ به ۵ ختم نمیشود
یکی از جذابترین حقایق دربارهی اعداد اول، الگوهای منحصربهفرد آنها است. برای مثال هر عدد اول بزرگتر از ۵ که به ۵ ختم شود، عدد اول نیست.
جمعبندی
عدد اول به عددی گفته میشود که تنها بر خودش و یک بخشپذیر است. روشهای متعددی برای کشف اعداد اول وجود دارد بااینحال هرچقدر به سمت اعداد بزرگتر برویم، یافتن اعداد اول نیز دشوارتر خواهد شد. اعداد اول در زمینههای مختلفی از نظریهی اعداد گرفته تا امنیت سایبری و ارتباط از راه دور کاربرد دارند.