آموزش
انواع توابع قدرمطلقی
توابع«گلدانی» و «سرسره ای»
خلاصه :
در این مطلب می خواهیم به دوتا از مهم ترین و پر کاربرد ترین توابع قدر مطلقی بپردازیم ، همچنین با ضابطه و طریق رسم شان آشنا شویمبِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيمِ
اول از تابع گلدانی آغاز می کنیم
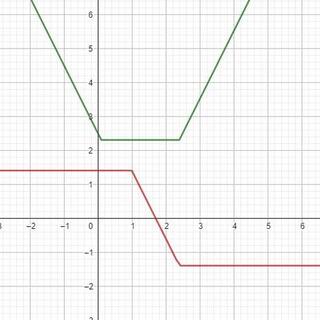
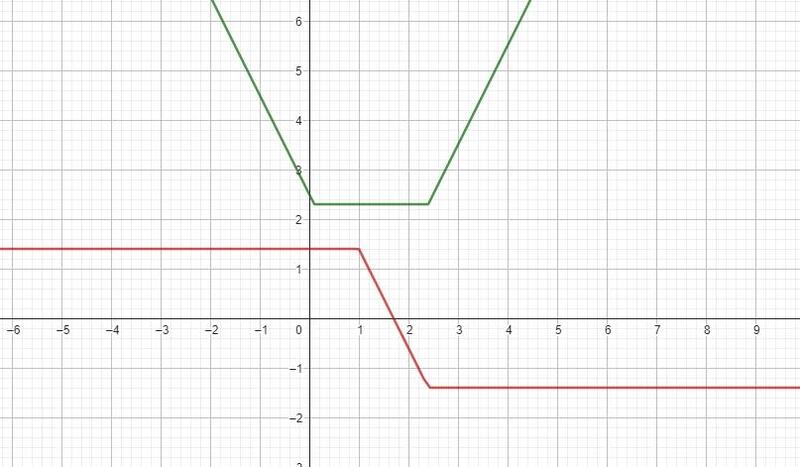
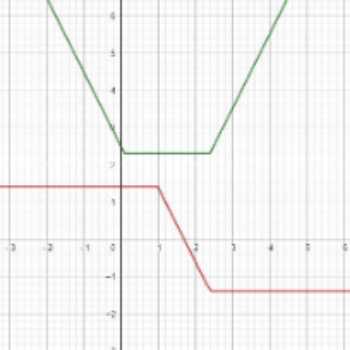
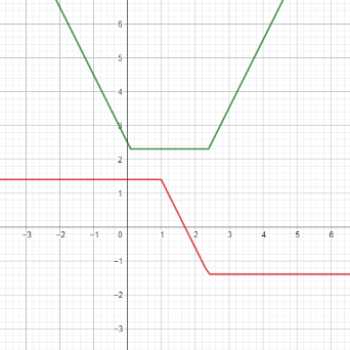
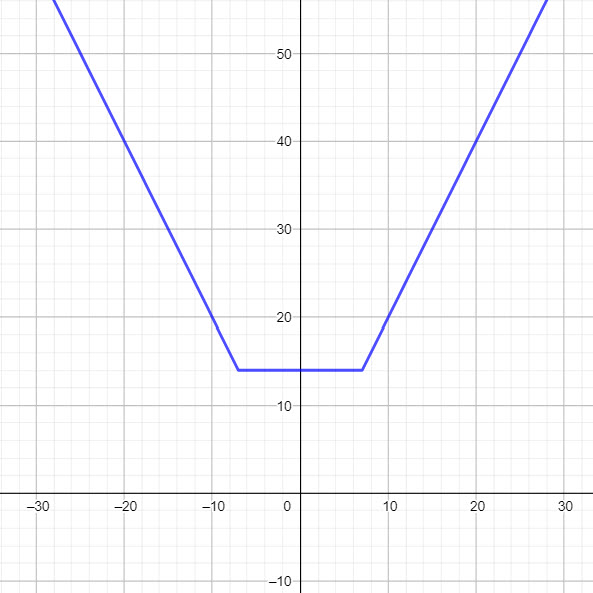
نمودارِ ضابطه y=|x-α|+|x-β| (α<β) ، به نمودار گلدانی معروف است. زیرا شکل آن شبیه به یک گلدان می باشد
-
شیب خط سمت راست (|x-β|) برابر با 2 و شیب خط سمت چپ (|x-α|) برابر با 2- می باشد. معادله خط صاف به صورت y=β-α خواهد بود.
-
اگر یک خط افقی مانند y = k ، نمودار گلدانی را قطع کند و موازی با خط کف نمودار گلدونی باشد، و به عبارتی دیگر اگر این خط در دو نقطه نمودار را قطع کند ،
آن گاه اندازه خط حاصل از دو نقطه ای که نمودار گلدونی را قطع کرده اند، برابر با k خواهد بود.
✅ راه رسم نمودار گلدانی :
- ابتدا ریشه های ضابطه را به وسیله جدول تعیین علامت به دست می آوریم. اولین مرحله پیدا کردن ریشه های ضابطه می باشد.
- سپس با استفاده از ریشه های به دست آمده و استفاده از جدول تعیین علامت سه ضابطه فرعی را از ضابطه اصلی پیدا میکنیم
- بعد بر اساس ضابطه های برآمده از جدول تعیین علامت، نمودار هریک را رسم کرده و قسمت صحیحش را بنا بر شرط ضابطه مشخص میکنیم
- مشاهده میشود قسمت های مشخص شده تشکیل یک گلدان می دهند
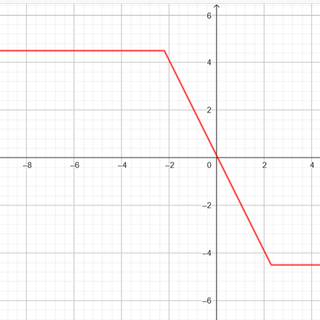
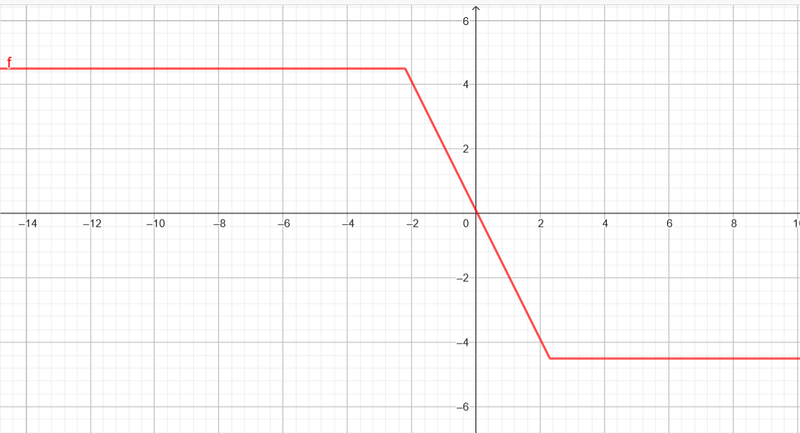
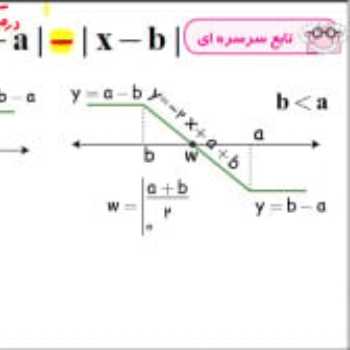
و اما تابع سرسره ای
|y=|x-α|+|x-β اگر در این ضابطه دو قدر مطلق را از هم کم کنیم تابع ما تبدیل به تابع سرسره ای می شود در نتیجه
دو تابع گلدانی و سرسره ای ضابطه هایی شبیه بهم دارند. ضابطه تابع سرسره ای : |y=|x-α|+|x-β
📏 راه رسم نمودار سرسره ای :
- ابتدا ریشه های ضابطه را به وسیله جدول تعیین علامت به دست می آوریم. اولین مرحله پیدا کردن ریشه های ضابطه می باشد.
- سپس با استفاده از ریشه های به دست آمده و استفاده از جدول تعیین علامت سه ضابطه فرعی را از ضابطه اصلی پیدا میکنیم
- بعد بر اساس ضابطه های برآمده از جدول تعیین علامت، نمودار هریک را رسم کرده و قسمت صحیحش را بنا بر شرط ضابطه مشخص میکنیم
- مشاهده میشود قسمت های مشخص شده دو خط موازی محور X ها یکی با عرض مثبت و یکی منفی و یک خط شیب دار واصل این دو خط را تشکیل میدهند که شبیه به سرسره است.